22º día de clase: qué es una OCTAVA musical ¿Por qué hay 12 NOTAS musicales? Introducción a la ESCALA

Una OCTAVA en música es el intervalo que separa dos notas musicales cuyas frecuencias están en relación 2 a 1.

¡Toma Geroma pastillas de goma! 😓
¿Y ésto qué quiere decir?

Antes de explicarlo diremos además que:

También se le llama OCTAVA a la distancia de ocho GRADOS entre dos notas de la ESCALA DIATÓNICA NATURAL (que es la más conocida en la música de Occidente).
En éste caso se suele decir que ambas notas están a distancia de una OCTAVA.

Nota: aún no hemos dado lo que son las escalas, ni los grados (por si no os habíais dado cuenta 😉). Mucho más abajo os haré una leve introducción de lo que es una ESCALA MUSICAL, aunque mientras tanto tenemos que ir haciendo referencia a los nombres de ESCALA y de GRADO para que podáis entender lo que es una OCTAVA.

Vamos a analizar ahora las dos definiciones de OCTAVA, empezando por la segunda definición:

OCTAVA: DISTANCIA DE 8 GRADOS ENTRE DOS NOTAS DE UNA ESCALA

¿Qué quiere decir ésta frase?

Seguro que la ESCALA DIATÓNICA NATURAL de Do Mayor es la que más conocéis todos sin saber que se llama así (diatónica natural) 😊:
Do - Re - Mi - Fa - Sol - La - Si - DO

Escuchad la ESCALA de Do Mayor:


La nota DO la hemos añadido para "cerrar" la ESCALA. Es la misma nota Do pero más aguda, y por tanto no haría falta repetirla para determinar las notas pertenecientes a la ESCALA de Do Mayor.
Pero para nuestra explicación es necesario que veáis ese DO más agudo.

La ESCALA de Do Mayor no son sólo éstas pocas notas que hemos puesto en el anterior trocito de pentagrama. La escala de Do Mayor comprende todos los "Do - Re - Mi - Fa - Sol - La - Si" que nos podamos encontrar a lo largo de un teclado (o cualquier otro instrumento), o a lo largo de toda una partitura escrita y compuesta en la ESCALA de Do Mayor. En la siguiente imagen podéis ver cómo la ESCALA de Do Mayor se repite a lo largo de un pentagrama (en versiones más graves y más agudas), y eso que podríamos poner aún más notas por la parte izquierda y por la derecha, pero como ejemplo sirve:

Escuchad cómo vamos repitiendo la ESCALA de Do Mayor de GRAVE a AGUDO en la anterior imagen:

Los GRADOS son las diferentes notas de una ESCALA enumeradas en orden (por decirlo de alguna manera sencilla, pero en la clase correspondiente veremos mucho más sobre los GRADOS).

Los GRADOS se representan con números romanos, aunque en la siguiente imagen os he puesto las dos versiones para que os sea más cómodo:

Consiste simplemente en poner un número a cada nota de la ESCALA ante la que nos encontremos.
Aquí nos encontramos ante la ESCALA de Do Mayor y sus GRADOS son los que os he puesto. Do es el grado I, Re es el grado II, Mi es el grado III... Y DO vuelve a ser de nuevo el GRADO I (por ser la misma nota pero más aguda).
Pero si estuviésemos en otra escala distinta las notas que corresponderían a cada número de grado serían diferentes, obviamente. Lo veremos en la clase sobre las ESCALAS MUSICALES.
Cada nota de una ESCALA se llama GRADO. Y tiene un número de GRADO. Y conserva ese número de GRADO sea más grave o más aguda (como ocurre con Do y DO).
Todos los Do de la ESCALA de Do Mayor son el GRADO I
Todos los Re de la ESCALA de Do Mayor son el GRADO II
Todos los Mi de la ESCALA de Do Mayor son el GRADO III
Todos los Fa de la ESCALA de Do Mayor son el GRADO IV
... etc

OCTAVA: distancia de 8 GRADOS entre dos notas de la ESCALA.
Entre las notas Do y DO hay una OCTAVA de distancia, porque desde Do hasta DO (ambas incluídas) podemos contar 8 GRADOS.

Sólo como adelanto de información 😊 y para facilitaros la comprensión de lo que estamos explicando sobre la OCTAVA:

Al igual que existen distancias de OCTAVA, también tenemos distancias de PRIMERA, SEGUNDA, TERCERA, CUARTA, QUINTA, SEXTA, SÉPTIMA, (OCTAVA), NOVENA, DÉCIMA, ONCEAVA... etc.

Si entre Do y DO hay una OCTAVA de separación, o de distancia (porque podemos contar 8 GRADOS, ambas notas incluidas)...

¿Qué distancia habrá entre Do y Mi?
Pues hacemos lo mismo, contamos los grados incluyendo ambas notas: Do=un grado, Re=dos grados, Mi=tres grados. Hay 3 grados de distancia. Por lo tanto diremos que entre ambas notas hay una TERCERA de distancia.

¿Qué distancia habrá entre Re y Sol?
Contamos los grados entre Re y Sol (ambas incluídas): Re=un grado, Mi=dos grados, Fa=tres grados, Sol=cuatro grados. Hay 4 grados de distancia. Estamos ante una distancia de una CUARTA.

Los nombres de TERCERA, CUARTA, QUINTA,... OCTAVA ¿Os recuerdan a algo que hayáis oído alguna vez?
TERCERA menor, TERCERA mayor, CUARTA aumentada, OCTAVA disminuida... 😉
Pues ésto viene de contar los GRADOS de separación entre dos notas musicales de una ESCALA. Lo veremos en su momento, aún es pronto. Por ahora nos estamos centrando en lo que es una OCTAVA en general.

Hemos dicho que la ESCALA de Do Mayor comprende todas las notas "Do - Re - Mi - Fa - Sol - La - Si" que nos podemos encontrar en un teclado (o en cualquier otro instrumento), o que podemos escribir en un pentagrama. Unas veces esas notas serán más graves y otras veces más agudas.

Vamos a poner aquí de forma escrita la ESCALA de Do Mayor repetida solamente dos veces. Ya os habréis imaginado que cuando pongo mayúsculas es para reflejar que esas notas son más agudas:

Do - Re - Mi - Fa - Sol - La - Si - DO - RE - MI- FA- SOL - LA - SI ... continúa de nuevo.

Pues bien, no sólo habrá una OCTAVA de distancia entre las notas Do y DO sino que también habrá una OCTAVA entre Re y RE, entre Mi y MI, entre Fa y FA... etc. Contad la distancia que hay entre ellas incluyendo ambas notas. Y veréis cómo también contáis 8.

Entre cada nota de una ESCALA y la nota del mismo nombre inmediatamente más aguda (o más grave) SIEMPRE HABRÁ UNA OCTAVA DE DISTANCIA.

¿Habéis oído alguna vez la expresión: subir una OCTAVA a una canción o melodía?
Pues consiste simplemente en tocar las notas que tengamos en nuestra melodía pero una OCTAVA más "arriba", o más aguda (que es lo mismo).
Imaginad que estamos en la ESCALA de Do Mayor (como durante toda nuestra clase de hoy).
Tenemos una melodía que utiliza las notas "Do - Re - Mi - Fa - Sol - La - Si".
Por ejemplo, ésta:

Escucha:


¿Cuáles son las notas que están una OCTAVA más arriba que éstas? Pues son las notas con el MISMO NOMBRE que éstas, pero inmediatamente más agudas, como hemos estado viendo hasta ahora.
Hemos visto que desde Do hasta DO había 8 GRADOS (o notas de la ESCALA), incluyendo ambas notas al contarlos. Y pasaba lo mismo entre Re y RE, Mi y MI...etc.
Entonces sólo tenemos que coger cada nota y trasladarla a una OCTAVA de distancia, tocar cada nota una OCTAVA más arriba, y fijaos, las notas ahora tienen EL MISMO NOMBRE (son las mismas) pero más agudas:

Escucha:


Analicemos ahora la primera definición de OCTAVA que dimos al principio de nuestra clase:

OCTAVA: INTERVALO QUE SEPARA DOS NOTAS MUSICALES CUYAS FRECUENCIAS ESTÁN EN RELACIÓN 2 A 1

Pongamos de nuevo nuestra ESCALA de Do Mayor. Recordad que aquí sólo hemos puesto unas pocas notas y no todas las que podemos encontrarnos en un teclado, o en un pentagrama:

Nuestro primer Do es grave y el segundo DO es agudo. Escuchad los dos, Do y DO, por separado y después sonando a la vez:

Escuchad cómo cuando ambos suenan a la vez es como si se fundiesen en un sólo sonido. Casi no se nota que haya dos notas sonando juntas. Ésto es una característica que notaréis siempre cuando estéis ante dos notas separadas por una OCTAVA. Y ello ocurre porque una de ellas tiene exactamente EL DOBLE de frecuencia que la otra.

Recordemos que la FRECUENCIA es la cantidad de vibraciones POR SEGUNDO de un cuerpo sonoro (como por ejemplo una cuerda de guitarra). Se mide en hercios (hz), de tal manera que si yo tengo una cuerda que vibra a 440 hz, significa que vibra 440 veces CADA SEGUNDO. Imaginad lo rápido que tiene que vibrar esa cuerda para hacerlo 440 veces en un segundo.

El primer Do se produce gracias a que nuestra cuerda de guitarra, vibra determinadas veces cada segundo al ser pulsada con nuestro dedo cuando colocamos la nota Do. Y cuando pulsamos nuestra cuerda poniendo de nota el segundo DO, la cuerda vibra EL DOBLE DE VECES cada segundo que en el primero.
Nuestro segundo DO tiene EL DOBLE DE FRECUENCIA que el primero. Y al vibrar nuestra cuerda ahora muchas más veces por segundo, su sonido es más agudo.

Lo mismo ocurre con Re y RE, con Mi y MI, con Fa y FA... etc.

Por eso hemos definido al principio la OCTAVA como:
El intervalo que separa dos notas musicales (en nuestro ejemplo Do y DO) cuyas frecuencias están en relación 2 a 1 (es decir, que una es el doble de la otra).

Si tenemos dos notas a una distancia de una OCTAVA (recordad, separadas 8 GRADOS), la segunda nota siempre hará vibrar la cuerda el doble de veces por segundo que la primera.
Las notas que están a distancia de una OCTAVA tienen siempre el mismo nombre.

Contra más veces por segundo vibre una cuerda, más agudo será su sonido.
Contra menos veces por segundo vibre una cuerda más grave será su sonido.
Ésto ya lo vimos en nuestra clase sobre las frecuencias de las notas musicales.

Fijaos en la siguiente imagen en la que he puesto las frecuencias correspondientes a nuestras notas de ejemplo del día de hoy, que pertenecen a la OCTAVA nº4 de un teclado (más abajo veremos una imagen de todas las OCTAVAS en un teclado). La frecuencia que veis en cada nota es la cantidad de veces que nuestra cuerda de guitarra vibra cada segundo al poner esa nota en ella y pulsarla:

Como veis nuestro segundo DO tiene el doble de frecuencia que el primer Do.
Desde Do hasta DO las frecuencias de todas las notas van aumentando paulatinamente, poco a poco. Nuestra cuerda de guitarra, cada vez que ponemos las sucesivas notas en ella, va vibrando cada vez más deprisa al pulsarla (contra más deprisa vibre una cuerda de guitarra más AGUDA será la nota).

Y es todo el intervalo de notas (o frecuencias) que va desde Do hasta DO, el que conforma una OCTAVA. Es decir, que una OCTAVA va desde que tenemos una frecuencia determinada (en nuestro caso la de Do), hasta que llegamos al DOBLE de dicha frecuencia (en nuestro caso la de DO).
O lo que es lo mismo:
Una OCTAVA va desde que nuestra cuerda vibra x veces por segundo al pulsarla poniendo en ella una nota, hasta que vibra 2 veces x por segundo al pulsarla poniendo en ella la misma nota pero inmediatamente más aguda. Todas las posibles vibraciones de nuestra cuerda que estén entre medias de x y 2x (es decir, de ambas notas) pertenecen a esa OCTAVA.

En el caso de nuestra imagen anterior con las frecuencias de cada nota escritas, la OCTAVA iría desde que nuestra cuerda vibra 261,625565 hz (que es Do) hasta que vibra 523,251131 hz (que es DO).
La OCTAVA sería TODAS las vibraciones posibles entre ambas cantidades. Recordad la definición:
OCTAVA: el intervalo que separa dos notas musicales cuyas frecuencias están en relación 2 a 1. Todo el intervalo.

Voy a ejemplificar esto con lo que es un KILÓMETRO:
Un kilómetro iría desde que tenemos 0 metros hasta que tenemos 1000 metros. Todos los metros que estén entre medias de ambas cantidades pertenecen al mismo kilómetro.
Lo mismo ocurre con la OCTAVA: va desde que tenemos x vibraciones por segundo hasta que tenemos el doble de vibraciones por segundo. Todas las vibraciones que estén entre medias de ambas cantidades pertenecen a la misma OCTAVA.

Como ya hemos visto, una OCTAVA no tiene porqué empezar y terminar en notas Do. Siempre hay una OCTAVA entre dos notas del MISMO nombre, una de ellas inmediatamente más aguda que la otra.

Como estamos hoy con la OCTAVA 4ª de Do a DO, seguiremos nuestro ejemplo con ella.

La OCTAVA 4ª es la que véis coloreada de verde en éste piano de 88 teclas:

Esta es la distribución en OCTAVAS de un teclado.
Véis que el dibujo o diseño de TODAS las OCTAVAS es idéntico.
Y véis que sobran algunas teclas a derecha e izquierda del teclado que pertenecen a octavas incompletas (OCTAVA 8, una tecla y OCTAVA 0, 3 teclas).

Cada tecla o nota de la OCTAVA 2 tiene el doble de frecuencia que la misma tecla o nota en la OCTAVA 1.
Cada tecla o nota en la OCTAVA 3 tiene el doble de frecuencia que la misma tecla o nota en la OCTAVA 2.
Y así sucesivamente con todas.

Tenemos siempre las mismas notas en cada OCTAVA. Lo que ocurre es que a medida que vamos hacia la derecha del teclado, las OCTAVAS van siendo cada vez más agudas.

Es como si cada OCTAVA fuese un pequeño teclado independiente con 12 teclas o notas (contadlas).
Hemos cogido ese pequeño teclado y lo hemos duplicado 7 veces. Pero hemos afinado cada uno al doble de frecuencia que su anterior, con lo que nos han ido quedando cada vez más agudos.

Vemos en la OCTAVA 4ª escritas nuestras 8 notas de antes, que corresponden a las teclas blancas "casualmente" en éste ejemplo que estamos estudiando (Do - Re - Mi - Fa - Sol - La - Si - DO).
En otras ESCALAS se utilizan también las teclas negras.

Os habréis dado cuenta de que nuestra OCTAVA 4ª, coloreada de verde en el teclado anterior, tiene 12 teclas (al igual que el resto de OCTAVAS). Porque también están entre Do y DO las FRECUENCIAS de las notas de las teclas negras. Recordad que la OCTAVA era TODO lo que estuviese entre Do y DO (en nuestro ejemplo de hoy).

En el caso de la ESCALA de Do Mayor que estamos estudiando (recordad que aún no vimos las escalas) no tenemos que hacer uso de las teclas negras, pues todas las notas que componen la ESCALA de Do Mayor corresponden a teclas blancas.
Pero hay muchas otras ESCALAS que utilizan algunas o muchas teclas negras, ya que tienen notas con sostenido o bemol (que son las que se encuentran en las teclas negras).

PEQUEÑO RESUMEN:

Hasta aquí debemos tener claro que:

- Una OCTAVA es:

1) Absolutamente TODAS las notas musicales que se encuentren entre una nota determinada y la misma nota inmediatamente más aguda (que tiene el doble de frecuencia). En nuestro teclado hemos visto que la OCTAVA comprende todas las teclas blancas y negras que se encuentran entre ambas notas de referencia. En total una OCTAVA tiene 12 teclas o notas (ya veremos luego porqué son 12).

2) También se le llama OCTAVA a la distancia de 8 GRADOS entre dos notas de una ESCALA diatónica natural. Hay una OCTAVA de distancia siempre entre notas DEL MISMO NOMBRE una inmediatamente más aguda que la otra.

En nuestro teclado hemos visto que la ESCALA de Do Mayor: Do - Re - Mi - Fa - Sol - La - Si - DO sólo estaba compuesta por teclas blancas. Pero hay otras muchas ESCALAS que utilizan teclas negras al estar formadas por algunas notas con sostenido o bemol.

UNA OCTAVA TIENE REALMENTE 12 NOTAS

Las notas Do - Re - Mi - Fa - Sol - La - Si - DO conforman una escala diatónica natural, como he dicho antes (ésta es la escala de Do mayor). Por ahora no sabemos lo que es una ESCALA. Pero os diré, para ir introduciendo el tema, que:

Una ESCALA musical es "unas cuantas notas musicales que se escogen de entre las 12 notas que tiene realmente una OCTAVA en el sistema musical occidental" (recordad las 12 teclas que tenía cada OCTAVA en nuestro teclado anterior).

Y éstas notas musicales escogidas (las de la ESCALA) son las que se utilizan para componer cada canción, o melodía.
La ESCALA que hemos escogido nosotros durante toda esta clase de hoy es la de Do Mayor. De entre todas las 12 notas (o teclas blancas y negras) que tiene una OCTAVA nosotros hemos escogido las notas de la ESCALA de Do Mayor.

Uno no escoge las notas que quiere para formar una ESCALA, sino que cada tipo de escala (ya que hay varios) tiene ya su manera de saber qué notas exactamente se deben elegir. Pero ésto lo veremos cuando hablemos de verdad de las ESCALAS. Es muy fácil, ya lo veréis.

Las melodías o canciones que solemos escuchar no necesitan todas las 12 teclas o notas que tiene una OCTAVA. Sino que cada melodía o canción se toca con una determinada ESCALA de notas escogidas de entre esas 12, y no se suelen usar las teclas o notas que queden fuera de esa ESCALA.
Por ejemplo, si para tocar o cantar una canción o melodía escogemos la ESCALA de Do Mayor que hemos puesto hoy de ejemplo:
Do - Re - Mi - Fa - Sol - La - Si - DO
Tocaremos o cantaremos nuestra canción o melodía con esas notas nada más y no usaremos el resto de notas de la OCTAVA. Por ejemplo no usaremos Do#, ni Fa#, ni La♭...

La ESCALA determina el TONO en el que va a sonar nuestra melodía. ¿Nuestra melodía será alegre o triste?
Tenemos ESCALAS como Do Mayor (la que estamos viendo hoy), La menor, Re Mayor, Sol menor... y un largo etcétera.
Cada una de ellas imprime un determinado carácter a nuestras melodías.
Las ESCALAS MENORES denotan tristeza, suavidad, melancolía... y las ESCALAS MAYORES son alegres, tajantes, agresivas...

En otros sistemas musicales como el árabe, la OCTAVA tiene 24 notas (en lugar de 12 como el de Occidente) y por eso interpretan su música con sonidos que en occidente "no conocemos" (por decirlo de alguna manera).
Tendrán los instrumentos apropiados, es decir, que en un piano normal y corriente no podréis ver esas 24 notas en las que ellos dividen su OCTAVA, porque nosotros sólo tenemos 12 teclas (o notas) en nuestras OCTAVAS. Pero sí que podréis tocar alguna melodía que imite un poco dicha música árabe con nuestras 12 notas occidentales.

¿POR QUÉ HAY 12 NOTAS EN UNA OCTAVA?

Como la OCTAVA va desde una frecuencia x hasta que la frecuencia es 2 veces x (es decir, el doble), tendremos ahí multitud de posibles sonidos.
Imaginad que tengo una nota con frecuencia 10 hz (la cuerda al poner esa nota vibra 10 veces por segundo), la OCTAVA desde esa nota llegará hasta la versión inmediatamente más aguda de ella, que vibrará a 20 hz (el doble).
Mi OCTAVA irá desde el sonido que vibra a 10 hz hasta el sonido que vibra a 20 hz (que es la misma nota pero más aguda, como ocurría entre Do y DO). Todas las posibles vibraciones por segundo de mi cuerda que estén entre 10 hz y 20 hz forman parte de mi OCTAVA.

Entre medias de 10 hz y 20 hz tendremos muchos sonidos:
- 10,01 hz - 10,02 hz - 10,03 hz - 10,04 hz... y así podríamos seguir poniendo decimales y más decimales hasta llegar a 20 hz. Como veis tendríamos infinidad de sonidos, ya que cada vez que aumentamos la vibración de nuestra cuerda en un decimal el sonido es distinto. Pero el oído humano no distingue un sonido cualquiera de otro que vibre un simple decimal más deprisa. ¿Qué diferencia podríamos notar entre un sonido cuya cuerda vibrase 10 veces por segundo y otro en que vibrase 10,1 veces por segundo? Pues ninguna.
Para que el oído humano capte la diferencia de un sonido a otro tiene que haber más vibraciones de diferencia entre ellos. Y ésto es lo que hicieron los expertos en su día, elegir de entre toda la multitud de sonidos que puede haber dentro de una OCTAVA (miles), sólo unos cuantos que estaban separados entre si por x vibraciones.

Y dividieron la OCTAVA en 12 sonidos IMPORTANTES o que ellos consideraron que eran los más agradables a nuestro oído, haciendo una operación matemática que veremos en una próxima clase.

Es decir, que ahora en nuestro ejemplo, entre la nota que vibra a 10 hz y la que vibra a 20 hz, en lugar de tener infinidad de sonidos casi idénticos unos a otros, tendríamos sólo 12 sonidos que alguien escogió de entre todos ellos. Y esos 12 sonidos son los que se utilizan en nuestra música occidental. Unas veces estos 12 sonidos serán más agudos y otras veces serán más graves, pero en resumidas cuentas son los mismos todo el tiempo. Absolutamente toda la música que conocemos en occidente está formada con esos 12 sonidos, combinando unos con otros (excepto modernidades y cosas extrañas que pueda haber).

Esos 12 sonidos son lo que conocemos como nuestras notas musicales. En nuestro sistema musical occidental sólo tenemos 12 sonidos completamente diferentes:
Do - Do# (o Re♭) - Re - Re# (o Mi♭) - Mi - Fa - Fa# (o Sol♭) - Sol - Sol# (o La♭) - La - La# (o Si♭) - Si

Y con éstos 12 sonidos se componen todas las melodías y canciones que conocemos. Se elige de entre todos ellos la ESCALA que queramos, según el carácter que queramos dar a nuestra música, y se empieza a componer. ¿Queremos una melodía melancólica? Elegimos una ESCALA que sea "menor" (ya lo veremos en nuestra clase sobre las ESCALAS). ¿Queremos una melodía alegre? Elegimos una ESCALA "Mayor"...

Observad en la siguiente imagen cómo cada tecla negra puede tener 2 nombres distintos:
- o nombramos la tecla negra con el mismo nombre de la tecla blanca ANTERIOR y el símbolo SOSTENIDO (#)
- o nombramos la tecla negra con el nombre de la tecla POSTERIOR y el símbolo BEMOL (♭).
Los nombres que le demos a éstas teclas negras dependerán de la ESCALA que hayamos escogido para interpretar nuestra melodía. Lo veremos en clases posteriores.

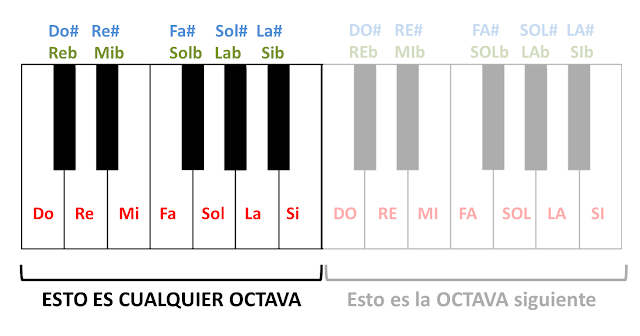
Los 12 sonidos que tenemos son éstos (contad todas las teclas que veis en donde pone "ESTO ES CUALQUIER OCTAVA", las teclas negras y las blancas):

Habréis contado 12 teclas ¿verdad? Y, como sabréis, esas MISMAS teclas se repiten de nuevo en un teclado varias veces (en la imagen anterior sólo he puesto una repetición).
En donde he puesto "Esto es la OCTAVA siguiente" vemos que el diseño es exactamente igual que el del que hemos contado las teclas. Incluso las notas se llaman igual y todo.
Ésto es porque éstas teclas que he dejado un poco transparentes suenan exactamente igual que las otras, lo que pasa es que son un poco más agudas que aquellas.
Y, como he dicho anteriormente, cada nota o tecla de la "OCTAVA siguiente" tiene el doble de frecuencia que la misma nota o tecla de la "OCTAVA anterior".
Ejemplos:
DO tiene el doble de frecuencia que Do
RE tiene el doble de frecuencia que Re
MI tiene el doble de frecuencia que Mi
FA# (o SOL♭) tiene el doble de frecuencia que Fa# (o Sol♭)
... etc

Vamos a escuchar dos OCTAVAS que vayan seguidas en un teclado para que comprobéis cómo suenan igual pero la primera OCTAVA más grave y la segunda más aguda. Oiréis 13 sonidos en cada audio (y no 12). Ésto es porque vamos a ir desde Do hasta DO para "cerrar" cada OCTAVA. Recordad que una OCTAVA en música es el intervalo que separa dos notas musicales cuyas frecuencias están en relación 2 a 1.

1) Una OCTAVA cualquiera que podría ser la que pone "ESTO ES CUALQUIER OCTAVA":



2) la OCTAVA siguiente que es inmediatamente más aguda que la que acabamos de oír:



3) Y ahora escucharemos las dos OCTAVAS juntas sonando a la vez, para que notéis cómo se funde el sonido de ambas y casi no se nota que estamos tocando dos OCTAVAS al mismo tiempo. Ello ocurre, como ya os he dicho, porque las notas de la segunda octava son idénticas a las de la primera, pero más agudas:

¿Y por qué si la OCTAVA tiene 12 notas hemos escuchado aquí 13?

Pues porque nuestra OCTAVA va de Do a DO. Y la nota DO en realidad es la nota que comienza la siguiente OCTAVA. Fijaos en la anterior imagen cómo la nota DO se encuentra ya en la zona transparente de nuestra imagen (en la que pone "Esto es la OCTAVA siguiente"). Por lo tanto pertenece ya a la siguiente OCTAVA. Pero a la vez es también la nota que "cierra" nuestra OCTAVA más marcada en la imagen anterior.

Comparémoslo con las 24 horas que tiene un día (como por ejemplo un sábado):
Un día tiene 24 horas, que van desde las 00:00 horas de una noche hasta que vuelve a marcar nuestro reloj las 00:00 horas en la noche siguiente. Y en éste momento es cuando empieza el siguiente día. Cuando el reloj marca las 00:00 horas justas ya decimos que empieza el domingo.

Y entonces si nuestro sábado acaba en cuanto dan las 00:00 horas de la noche siguiente, y ahí empieza también el domingo... ¿Esas 00:00 horas pertenecen al sábado o al domingo?

La respuesta sería que pertenecen al domingo. Nuestro sábado terminaría a las 23 horas, 59 minutos, 59 segundos... (23:59:59... horas), porque en cuanto diesen las 00:00 horas ya sería domingo.

Lo mismo ocurre cuando hablamos de las OCTAVAS. Si una OCTAVA cualquiera va de Do a DO, acaba en cuanto llega a DO, pero éste DO pertenece ya a la OCTAVA siguiente. Ese DO cierra mi OCTAVA inicial, pero también abre mi siguiente OCTAVA.

OCTAVA COMO MEDIDA "ESTÁNDAR": DISTRIBUCIÓN DE TODAS LAS NOTAS QUE EXISTEN EN OCTAVAS DE DO

Siempre vemos en los libros ésta distribución en OCTAVAS en los teclados. La distribución estándar de todos los sonidos en cualquier instrumento (y no sólo en el teclado) está hecha en base a las OCTAVAS de Do:

Habréis visto nombrar notas de la siguiente manera:
Do4, Re5, Fa6... etc.
Ésta manera de nombrar las notas significa (en los 3 ejemplos que acabo de poner):
Do4 - Es el Do de la 4ª OCTAVA. El Do de la OCTAVA que hemos coloreado de verde.
Re5 - Es el Re de la 5ª OCTAVA. El Re de la OCTAVA que hemos coloreado de azul clarito.
Fa6 - Es el Fa de la 6ª OCTAVA. El Fa de la OCTAVA que hemos coloreado de azul oscuro.
Etc, etc... con todas las notas.

Es decir, que para nombrar las diferentes notas musicales que existen, y saber a cuál de todas nos referimos, las notas "occidentales" se "agrupan" en OCTAVAS de Do.

A cualquier músico que le digan "toca el Mi de la 5ª OCTAVA" ya sabe a qué Mi se refieren.
Si no se dividiesen todas las notas que existen en "grupitos concretos", a ese músico le tendrían que decir "toca el Mi correspondiente a la tecla 56 de un teclado" 😢. El músico tendría que contar teclas como un loco. Sin embargo, con la división de los sonidos en OCTAVAS de Do, el músico sólo tiene que conocer el "dibujo o diseño" de la OCTAVA de Do, y en un sólo golpe de vista sabe cuál es la OCTAVA 5ª para tocar ese Mi.

El porqué se decidió utilizar la OCTAVA de Do como "medida estándar" lo desconozco. He buscado en internet y no encuentro respuesta. Si la encuentro alguna vez os la pondré en una nueva entrada.
Aunque lo verdaderamente importante es que conozcáis ésta división que los músicos hacemos de todas las notas que existen en OCTAVAS de Do, porque oiréis o leeréis MUCHAS VECES aquello de:
La3, Re2... el Sol de la OCTAVA 1... etc.

Os vuelvo a recordar entonces, ya que ahora tenemos 3 maneras de ver la OCTAVA:

- OCTAVA como DISTANCIA de 8 grados entre 2 notas de una ESCALA (Do-DO, Re-RE, Mi-MI...)

- OCTAVA como TODAS LAS NOTAS (o teclas) QUE EXISTEN entre una nota cualquiera y la misma nota pero inmediatamente más aguda.
Son 12 notas (12 teclas). Es decir, todas las notas que podemos encontrarnos entre una nota cualquiera y la nota que tiene el doble de FRECUENCIA que ella son 12, porque alguien en su momento "eliminó" de la OCTAVA todos aquellos sonidos demasiado similares entre sí y dejó solo los más agradables.

- OCTAVA como división estándar de todas las notas existentes para poder referirnos a cualquier nota de una manera cómoda. Se ha elegido la OCTAVA de Do como referencia.

Y LAS NOTAS QUE "SOBRAN" A AMBOS LADOS DE UN TECLADO... ¿A QUÉ OCTAVA PERTENECEN?

Todas las notas siempre tienen su versión inmediatamente más aguda, con el doble de FRECUENCIA que ella. Cualquier tecla que veais en un teclado siempre tiene otra tecla con su mismo nombre de nota, y que es más aguda (o grave) que ella.
¿Qué ocurre entonces con la OCTAVA 7 de nuestro teclado, coloreada de violeta? ¿Es que sus notas o teclas no tienen una versión inmediatamente más aguda? No vemos por ninguna parte una OCTAVA 8.

Lo que ocurre es que si nuestro piano tuviese una OCTAVA 8, las notas de ésta OCTAVA 8 serían MUY agudas, y no suele hacerse música con notas tan agudas.
Lo mismo ocurre con la OCTAVA 1, vemos que a su izquierda no tenemos lo que podríamos llamar OCTAVA 0. Si tuviésemos en nuestro piano una OCTAVA 0, sus notas serían tan graves que producirían una música "fea".
Nuestro teclado de la imagen tiene 88 teclas (como casi todos los pianos). Y en esas 88 teclas nos caben 7 OCTAVAS, y tenemos también además, sin colorear, unas teclas que "sobran" a la izquierda y a la derecha del teclado. Esas notas "sobrantes" pertenecen eso sí, a las OCTAVAS 0 y 8 respectivamente, aunque dichas OCTAVAS no estén completas.

La única tecla que vemos en nuestra supuesta OCTAVA 8 es la nota Do, porque es la que sigue continuando el mismo orden que lleva el teclado. Ésta nota, si tenemos que referirnos a ella diremos: "Do8" o "el Do de la OCTAVA 8".
Las 3 teclas de nuestra supuesta OCTAVA 0 son: La, La# (o Si♭) y Si, que también son las notas que siguen el mismo orden que todas las demás en el teclado. Y a ellas nos referiremos como: La0, La#0 (o Si♭0) y Si0. También como "el La de la OCTAVA 0"... etc.

Aunque casi todos los pianos tienen 88 teclas, hay pianos "raros" que tienen 97 teclas, como puede ser el Bösendorfer 290 Imperial, que tiene una OCTAVA 0 completa, cuyas teclas "añadidas" están todas pintadas de negro para distinguirlas de las teclas "normales" que puede tener un piano de 88 teclas:

Esta OCTAVA 0 de éste piano suena MUY grave (sus 12 notas tienen unas frecuencias MUY bajas, vibran MUY despacio sus cuerdas). En el Bösendorfer 290 Imperial se tocan composiciones musicales escritas exclusivamente para tal gravedad de sonido.

Aquí tenéis un vídeo del canal de Mark959 en el que podemos escuchar cómo suenan esas notas tan sumamente GRAVES:

Como decía, todas las notas siempre tienen su versión inmediatamente más aguda (o más grave, por supuesto), pero en algunos instrumentos no podremos tocar muchas de ellas por no estar "presentes" en él al no ser adecuadas para el sonido de ese instrumento.